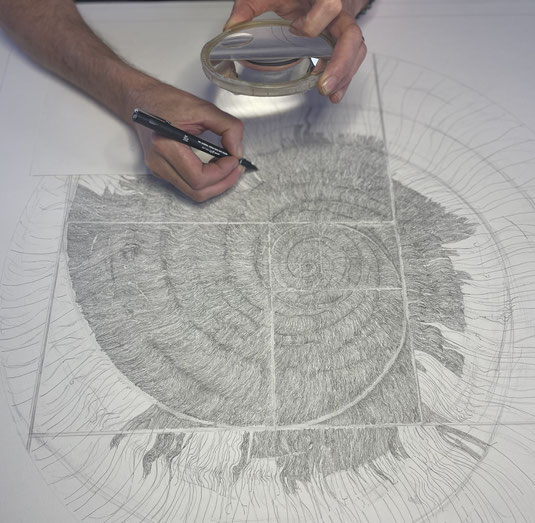
Protocole

En 2022, j’ai réalisé une série de plusieurs grands dessins reproduisant des captures microscopiques de coupe de cellules s’inscrivant dans un cercle et faisant apparaître leur structure géométrique précise (Rhombe, tessellation, hexagone…). Celle de la suite de Fibonacci est également manifeste et explicite dans la nature, à des échelles variables. On peut recenser sa présence dans de multiples variétés végétales mais aussi de façon plus surprenante dans l’enroulement des tornades ou le mouvement des galaxies. Cette poétique du « microscopique » se confondant avec la complexité de l’univers suffit à aiguiser ma curiosité. Dans le monde organique, cette dimension mathématique est proprement vertigineuse. J’ai fait des recherches sur les coquilles de nautile, les tests de foraminifères, sur les amanites de phylloceras, les céphalopodes et autres mollusques à l’état fossile dont le schéma des structures alvéolaires est mesurable. J’ai donc commencé par étudier le mécanisme de la suite en me plongeant dans sa définition mathématique. J’ai ensuite élaboré un plan de travail pour improviser une nouvelle cellule reprenant cette curieuse courbe infinie.

« j’ai considéré le chiffre 1 comme équivalent à une heure de travail.

A partir de cette base, j’ai décidé de décliner la suite en respectant son mécanisme de croissance. J’ai exclu tout modèle de représentation et toute mimétique. Je n’avais donc au préalable aucune idée précise de mon dessin final. Je me suis laissé porter par mes découvertes.

J’ai simplement disposé sur mon mur d’étude tous les travaux que j’avais pu réaliser sur le sujet et toutes les informations que j’avais pu recenser.

J’ai inscrit le jour et l’heure à laquelle j’ai décidé de commencer la réalisation, en bas de ma feuille. Le 8 mai 2025 à 8 heure du matin.

J’ai considéré ma feuille blanche et mes outils comme le 0 associé au 1

« Comme j’ai pu le lire, j’ai fait débuter la suite à 1 : f 0 = f 1 = 1 , f 2 = 2 , f 3 = 3 , f 4 = 5 , etc. Le nombre F_n s'appelle parfois le n-ième nombre de Fibonacci, bien qu'il soit techniquement le n+1-ième si on commence à 0 ».

J’ai donc commencé par réaliser le dessin et par esquisser au crayon le mouvement de la suite durant l’heure 1

J’ai commencé mon travail à l’encre noire durant l’heure 2

Pour arriver à 3, j’ai travaillé une heure de plus.

Pour arriver au chiffre 5 , j’ai travaillé 2 heures.

Pour arriver au chiffre 8 , j’ai dessiné durant 3 heures.

Pour arriver au nombre 13 , j’ai travaillé durant 5 heures.

J’ai pris un temps d’observation pour constater l’avancé de mon esquisse et la surface de papier couverte en respectant scrupuleusement cette marge de 13 heures. 

J’ai réalisé ces premières séquences sans interruption notamment dans la dernière phase de 5 heures 

Habitué au dessin et maîtrisant ma méthode, j’ai considéré que deux séances supplémentaires ( de 8 heures puis de 13 heures) me permettrait d’arriver au nombre 34.

Ce constat me convenait bien. 34 est le chiffre récurrent du carré magique.

J’ai désormais un temps imparti pour le faire. Je dois improviser une cadence.

 J’ai ainsi décidé d’appeler cette cellule totalement imaginaire : « Melencolia », en hommage à DÜRER et à sa fameuse gravure .

 Pour en conserver une trace, j’ai demandé à mon épouse de me filmer et de me photographier ».

 A terme, j'ai aussi réalisé la suite 13, la suite 21 et la suite 55.